日本国債金利の主成分分析

マイナス金利や長短金利操作付き量的・質的金融緩和導入など、今年も何かと金融政策の変更とそれに伴う金利の変動がニュースを賑わせた一年でした。 久々に何か分析ネタを…ということで、日本国債金利を主成分分析することで、金利の構造の主なファクターが2016年はどのように推移したのかを調べたいと思います。

データはQuandlから持ってきます。 Quandlパッケージを使えば、data.frameやxtsなどの形でデータを使えるようになり、手軽に分析を始めることができます。

まずは、必要なライブラリを読み込みます。

library(Quandl)
library(dplyr)
library(tidyr)
library(ggplot2)
library(scales)

Quandlからデータを取ってくるには、データを表すコードと取得開始日を最低限入れます。 ここでは、日本国債金利データをそのままを使うことにします。 金利の変動について分析を行いたい場合は、Quandl関数のtransformでdiffを指定することで取ってくることができます。

irate <- Quandl("MOFJ/INTEREST_RATE_JAPAN", order = "asc", start_date = "2016-01-01")

取ってきたデータを確認します。

> head(irate)
        Date     1Y     2Y     3Y     4Y    5Y    6Y
1 2016-01-04 -0.042 -0.028 -0.014  0.003 0.026 0.036
2 2016-01-05 -0.043 -0.030 -0.014  0.003 0.026 0.036
3 2016-01-06 -0.044 -0.029 -0.014  0.002 0.022 0.032
4 2016-01-07 -0.045 -0.028 -0.014 -0.003 0.016 0.027
5 2016-01-08 -0.045 -0.031 -0.018 -0.003 0.016 0.022
6 2016-01-12 -0.048 -0.028 -0.018 -0.003 0.017 0.016
     7Y    8Y    9Y   10Y   15Y   20Y   25Y   30Y   40Y
1 0.059 0.120 0.186 0.264 0.599 0.986 1.150 1.282 1.402
2 0.059 0.120 0.181 0.259 0.588 0.971 1.135 1.264 1.386
3 0.055 0.115 0.176 0.253 0.583 0.967 1.131 1.260 1.382
4 0.049 0.110 0.171 0.245 0.573 0.958 1.116 1.238 1.363
5 0.039 0.101 0.161 0.230 0.557 0.939 1.096 1.220 1.346
6 0.034 0.097 0.157 0.221 0.548 0.930 1.086 1.207 1.338

1年から40年満期までの金利データが取れました。 早速、データを可視化します。

irate %>% 
  gather(Maturity, Rate, -Date) %>%
  mutate(Maturity = factor(.$Maturity, levels = paste0(c(1:10, 15, 20, 25, 30, 40), "Y"))) %>%
    ggplot(aes(x = Date, y = Rate)) +
    geom_line(aes(colour = Maturity), size = 1) + 
    scale_x_date(labels = date_format("%y/%m"), date_breaks = "3 month") +
    guides(colour = guide_legend(reverse = TRUE))

１月のマイナス金利導入以降、イールドカーブ全体的に低下傾向となり、２月終盤からは10年満期以下の国債の金利が全てマイナス圏で推移するようになります。 ７月には15年満期の国債の金利もマイナスという状態も見られるようになり、年間を通して一番金利が低下した時期であったことがわかります。 それ以降は全体的に上昇し、アメリカの大統領選挙後には、10年満期の国債の金利もマイナス圏から脱し、金利の上昇が加速しているように見えます。

それでは、このデータに対して主成分分析を行います。 これらの分析については、様々なところで行われているため詳細な説明は省きますが、金利は水準(Level)、傾き(Slope)、曲率(Curveture)の３つのファクターでほぼその構造が説明できると言われています。主成分分析によって、これらのファクターが導出されるのかを確認し、その時系列推移を可視化してみます。

特にひねりを加えるわけでもなく、Rのprcompを金利データに適用します。

irate_pc <- irate %>% 
  select(-Date) %>%
  prcomp(scale. = TRUE)

主成分分析を適用した結果を見てみます。

> summary(irate_pc)
Importance of components:
                         PC1     PC2     PC3     PC4     PC5
Standard deviation     3.654 0.99449 0.75082 0.24082 0.13649
Proportion of Variance 0.890 0.06593 0.03758 0.00387 0.00124
Cumulative Proportion  0.890 0.95589 0.99347 0.99734 0.99858
                           PC6     PC7     PC8     PC9    PC10
Standard deviation     0.09270 0.07582 0.05226 0.03636 0.03167
Proportion of Variance 0.00057 0.00038 0.00018 0.00009 0.00007
Cumulative Proportion  0.99915 0.99953 0.99972 0.99980 0.99987
                          PC11    PC12    PC13    PC14    PC15
Standard deviation     0.02533 0.02314 0.01826 0.01654 0.01175
Proportion of Variance 0.00004 0.00004 0.00002 0.00002 0.00001
Cumulative Proportion  0.99991 0.99995 0.99997 0.99999 1.00000

第３主成分までで累積寄与率が99％となり、ほぼこの３つでイールドカーブの構造を説明できていることがわかります。 主成分得点は以下のようになりました。

> head(irate_pc$x)
           PC1        PC2       PC3         PC4        PC5
[1,] -9.534255 -0.3139355 0.4521807 -0.16670843 -0.2093294
[2,] -9.425388 -0.2323307 0.4851745 -0.16565373 -0.1661761
[3,] -9.329534 -0.2554974 0.5167301 -0.11327598 -0.1747176
[4,] -9.152626 -0.2405698 0.5779134 -0.08359126 -0.2015301
[5,] -8.915227 -0.2231325 0.6567429 -0.03116720 -0.1449082
[6,] -8.801091 -0.1916643 0.7010752  0.05046791 -0.1497915
               PC6          PC7          PC8         PC9         PC10
[1,] -0.0451359411  0.057984040 -0.006210947  0.03531776  0.006980638
[2,] -0.0351578833  0.054768411  0.009829469  0.03076594  0.008573947
[3,] -0.0347377299  0.033557155  0.012547679  0.03020654  0.010608943
[4,] -0.0531471021 -0.004868424  0.018739106  0.05401370 -0.006719837
[5,] -0.0005787395  0.023142080  0.005714631  0.02306513 -0.002223937
[6,] -0.0028323655  0.009862543 -0.014780631 -0.01505679 -0.007297795
            PC11        PC12          PC13         PC14       PC15
[1,] -0.02586290 -0.03433084 -0.0009471546 -0.016075984 0.02848080
[2,] -0.03508559 -0.03784112  0.0147360705 -0.012732611 0.02126039
[3,] -0.02178643 -0.04119171  0.0143781817 -0.010653086 0.02193993
[4,] -0.02087492 -0.02625881  0.0161335068 -0.015374304 0.01088626
[5,] -0.01278054  0.01291703  0.0168199370 -0.008567272 0.02197490
[6,] -0.02024915  0.05001019  0.0143638963 -0.011216030 0.01494438

そして、各満期に対するファクターローディングスを見てみます。

data.frame(irate_pc$rotation[, 1:3]) %>%
  mutate(Maturity = factor(rownames(.), levels = rownames(.))) %>%
    gather(PC, FactorLodings, -Maturity) %>%
    ggplot(aes(x = Maturity, y = FactorLodings)) + 
    geom_line(aes(colour = PC, group = PC), size = 1) 

第１から第３主成分までが金利の水準、曲率、長短期の傾きをそれぞれ表していることがわかります。 （横軸の間隔が満期に対応して一定ではないので、形がちょっと変な感じですが…）

さらに、これらのファクターの時系列推移も可視化して、一年を通してどのように変動したのかを見てみます。

data.frame(Date = irate$Date, irate_pc$x[, 1:3]) %>% 
  gather(PC, Factor, -Date) %>%
    ggplot(aes(x = Date, y = Factor)) + 
    geom_line(aes(colour = PC), size = 1) +
    scale_x_date(labels = date_format("%y/%m"), date_breaks = "3 month")

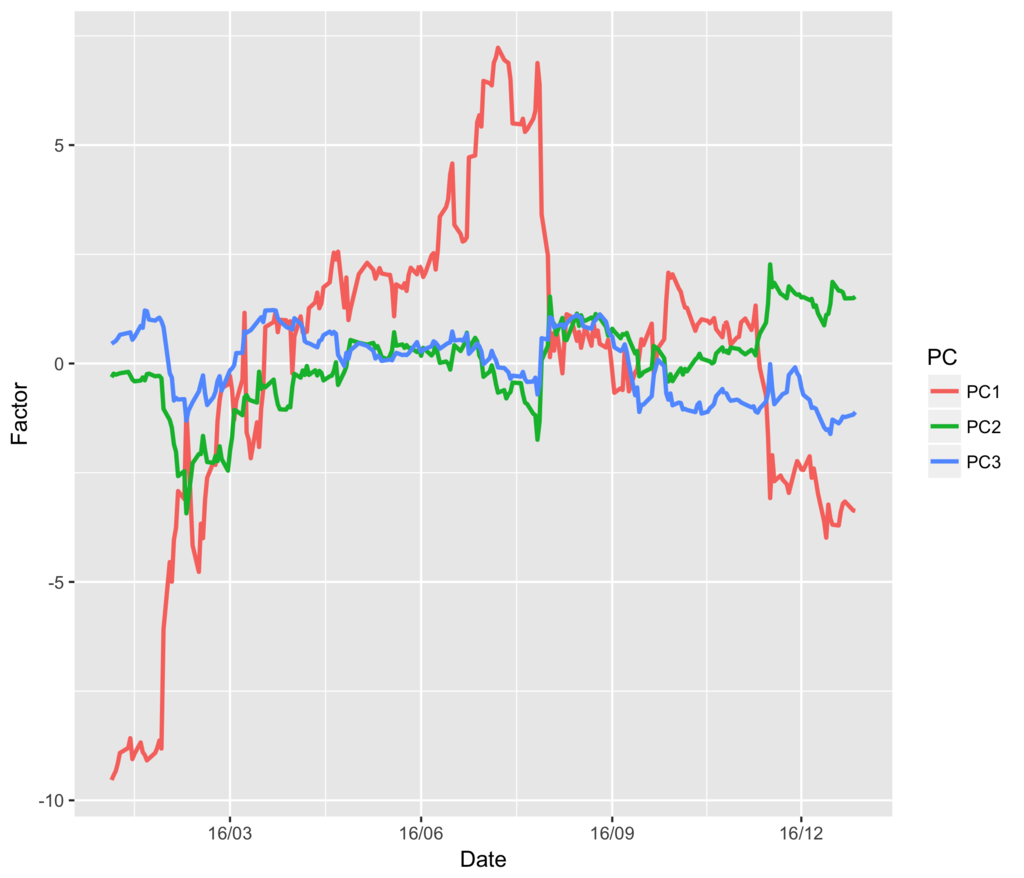
１月のマイナス金利導入以降、金利の水準が大きく下落し、傾きや曲率も変動したことがわかります。 そして、年後半には再び水準が上昇したことがわかります。 年間を通して、金利が下落した後に上昇して戻ってきたと言っても、 水準と傾き、曲率の３つのファクターを見ると、年初と年末ではイールドカーブの構造が異なっていることがわかります。

ただ単純に主成分分析しただけのものなので、ガチなフラットナー/スティープナーといった金利関連の取引に役立つわけではないと思いますが、データの取得から可視化、分析手法適用までRを使って簡単に始められますというものでした。

来年も世界各国の政治イベントで大きな動きがありそうということで、勝手にデータ分析の材料を提供してくれると思うと楽しめそうです。